O’Que Sao Numeros Primos Exemplos? Mergulhe no fascinante mundo dos números primos, explorando sua definição, propriedades e aplicações. Esses números, que possuem apenas dois divisores (1 e eles mesmos), desempenham um papel fundamental na matemática, ciência da computação e criptografia.
Desde a antiguidade, matemáticos se dedicam a desvendar os mistérios dos números primos, buscando padrões e propriedades que os tornam tão especiais.
Neste guia, vamos desvendar o conceito de números primos, apresentar exemplos e discutir suas aplicações em áreas como criptografia e teoria dos números. Você aprenderá métodos para identificar números primos, como o Crivo de Eratóstenes, e compreenderá a importância desses números na construção de outros números inteiros.
Prepare-se para uma jornada instigante pelo mundo dos números primos!
O que são números primos?
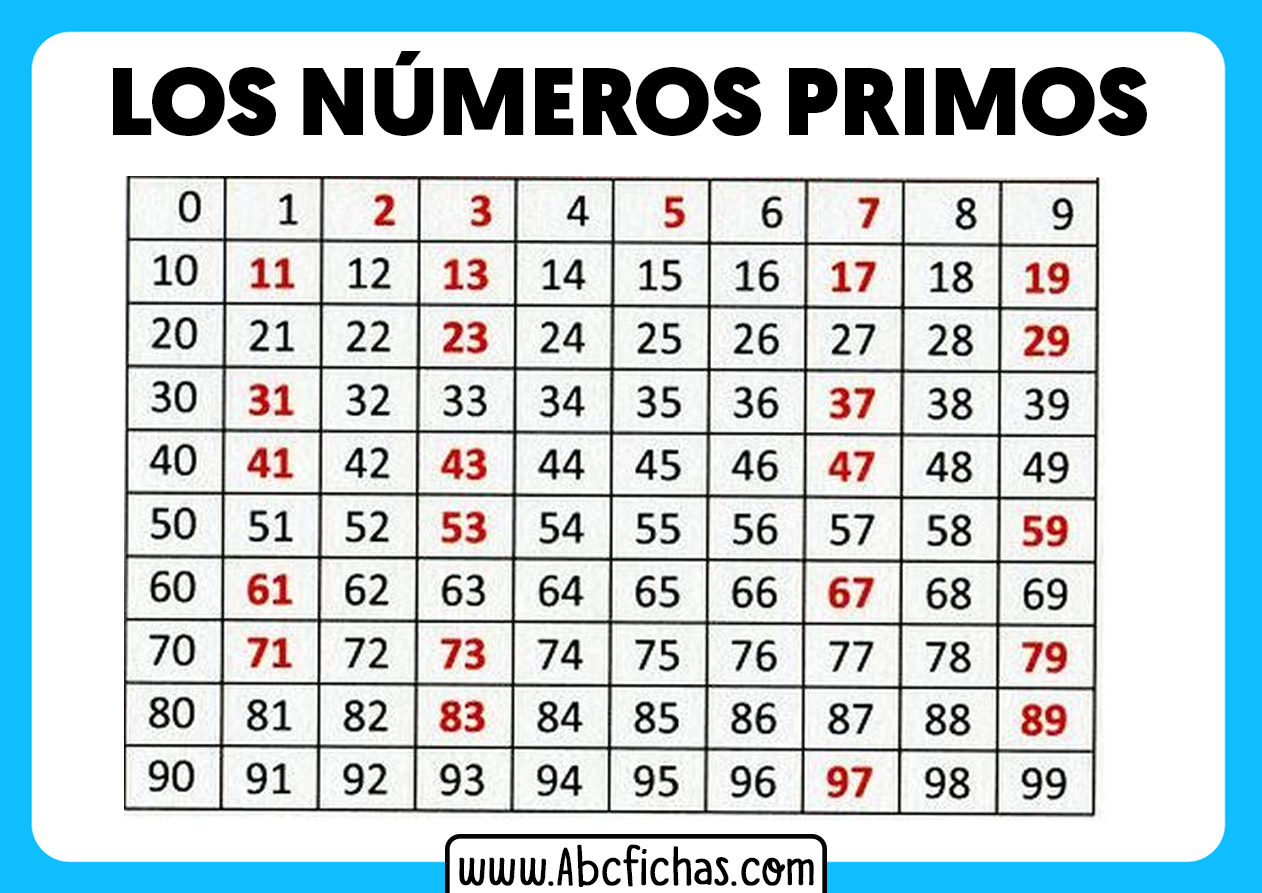
Números primos são os blocos de construção básicos dos números inteiros. Eles desempenham um papel crucial na matemática, ciência da computação e criptografia. Para entender a importância dos números primos, precisamos primeiro entender o que os define.
Um número primo é um número inteiro maior que 1 que tem exatamente dois divisores: 1 e ele mesmo. Em outras palavras, um número primo só pode ser dividido igualmente por 1 e por si mesmo. Os primeiros números primos são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, e assim por diante.
Números primos: exemplos e aplicações
Para ilustrar melhor o conceito de números primos, vamos analisar alguns exemplos e suas aplicações:
| Número | Divisores | Primo? | Aplicações |
|---|---|---|---|
| 2 | 1, 2 | Sim | Criptografia, teoria dos números |
| 4 | 1, 2, 4 | Não | – |
| 7 | 1, 7 | Sim | Ciência da computação, teoria dos números |
| 12 | 1, 2, 3, 4, 6, 12 | Não | – |
Os números primos têm aplicações em várias áreas, incluindo:
- Criptografia:A fatoração em números primos é a base da criptografia de chave pública, que é usada para proteger informações confidenciais, como transações online e comunicações. A dificuldade de fatorar números grandes em números primos garante a segurança desses sistemas.
- Teoria dos números:Os números primos são fundamentais na teoria dos números, que lida com as propriedades dos números inteiros. Eles são usados para provar teoremas, resolver equações e explorar padrões em números.
- Ciência da computação:Os números primos são usados em algoritmos de hash, geração de números aleatórios e criptografia. Eles também são usados para otimizar cálculos e melhorar a eficiência de programas de computador.
Como identificar números primos
Existem vários métodos para identificar números primos. Um dos métodos mais conhecidos é o Crivo de Eratóstenes, um algoritmo antigo que permite encontrar todos os números primos até um determinado limite.
O Crivo de Eratóstenes funciona da seguinte maneira:
- Crie uma lista de números inteiros de 2 até o limite desejado.
- Comece com o número 2, que é o primeiro número primo. Marque todos os múltiplos de 2 como não primos (4, 6, 8, etc.).
- Mova para o próximo número não marcado, que é 3. Marque todos os múltiplos de 3 como não primos (6, 9, 12, etc.).
- Continue este processo, marcando os múltiplos de cada número primo subsequente até atingir o limite desejado.
- Os números restantes na lista que não foram marcados são os números primos.
O Crivo de Eratóstenes é um método eficiente para encontrar números primos até um determinado limite. Ele é usado em várias aplicações, incluindo a geração de tabelas de números primos e a implementação de algoritmos de criptografia.
Números primos e seus usos na matemática
Os números primos possuem propriedades importantes que os tornam fundamentais na matemática. Uma dessas propriedades é o Teorema Fundamental da Aritmética, que afirma que todo número inteiro maior que 1 pode ser escrito de forma única como um produto de números primos.
Por exemplo, o número 12 pode ser fatorado em 2 x 2 x 3. Este teorema é fundamental para a compreensão da estrutura dos números inteiros e para a resolução de problemas matemáticos complexos. Os números primos também são usados na construção de outros números inteiros, como os números compostos, que são números inteiros maiores que 1 que não são primos.
Os números primos desempenham um papel crucial na matemática, permitindo a decomposição de números em seus fatores primos e fornecendo uma base para a construção de outros números inteiros.
A importância dos números primos na ciência da computação
“A criptografia moderna depende fortemente da dificuldade de fatorar números grandes em números primos.”
Ron Rivest, um dos criadores do algoritmo RSA.
A criptografia de chave pública, amplamente utilizada para proteger informações confidenciais, baseia-se na dificuldade de fatorar números grandes em números primos. O algoritmo RSA, um dos algoritmos de criptografia de chave pública mais populares, usa dois números primos grandes para gerar uma chave pública e uma chave privada.
A dificuldade de fatorar o produto desses dois números primos garante a segurança do sistema.
A segurança de sistemas de comunicação e transações online depende fortemente da dificuldade de fatorar números grandes em números primos. Os números primos desempenham um papel crucial na segurança da informação e na proteção de dados confidenciais na era digital.
FAQ Guide: O’Que Sao Numeros Primos Exemplos
Qual é a diferença entre um número primo e um número composto?
Um número primo é um número natural maior que 1 que é divisível apenas por 1 e por ele mesmo. Um número composto é um número natural maior que 1 que tem mais de dois divisores.
Quais são os primeiros 10 números primos?
Os primeiros 10 números primos são: 2, 3, 5, 7, 11, 13, 17, 19, 23 e 29.
O número 1 é um número primo?
Não, o número 1 não é considerado um número primo. Por definição, um número primo deve ter exatamente dois divisores, e o número 1 tem apenas um divisor, que é ele mesmo.

